تجميع K-means في تعلم الآلة: الأساسيات والتطبيق

مقدمة عن تجميع K-means

تجميع K-means هو خوارزمية شائعة في مجال تعلم الآلة غير المراقب (Unsupervised Learning)، تُستخدم لتقسيم مجموعة من البيانات إلى عدد محدد مسبقًا من المجموعات أو "التجمعات". تعتمد هذه الخوارزمية على فكرة أن كل نقطة بيانات تنتمي إلى التجمع الذي يكون متوسط النقاط فيه (أو المركز) هو الأقرب إليها. يُستخدم تجميع K-means على نطاق واسع في العديد من المجالات، مثل تحليل البيانات، وتصنيف النصوص، وتقسيم الصور، وتجزئة السوق.

تجميع K-means هو أحد أكثر خوارزميات التجميع استخدامًا في علوم البيانات. إنها طريقة لتحديد كميات النقاط بناءً على مجموعة من الملاحظات. الهدف هو تقسيم مجموعة من $n$ ملاحظة إلى $k$ مجموعة، حيث يتم تعيين كل ملاحظة إلى المجموعة التي يكون متوسطها (المركز) أقرب إليها. في هذه المقالة، سنتناول أساسيات تجميع K-means، وكيفية عمله، وتطبيقاته، ومعايير تقييمه، مع تقديم رؤى عملية.
$\mathrm{<span\; class="katex-mathml"><br></span>}$

أهداف التعلم

فهم تجميع K-Means: استيعاب المفهوم الأساسي وكيفية عمل تجميع K-means.

استكشاف خصائص المجموعات ومعايير التقييم: تعلم كيفية تقييم جودة المجموعات.

فحص التطبيقات الواقعية: اكتشاف كيفية استخدام K-means في مختلف المجالات.

تنفيذ تجميع K-Means في بايثون: الحصول على تجربة عملية بتنفيذ التجميع.

ما هو تجميع K-Means؟

تجميع K-means هو خوارزمية تعلم غير مُراقب مصممة لتقسيم البيانات إلى عدد محدد من المجموعات. تعمل الخوارزمية عن طريق تقليل التباين داخل كل مجموعة، والذي يُقاس كمجموع المسافات المربعة من كل نقطة إلى مركز مجموعتها.

المكونات الرئيسية:

المراكز Centroidsالنقاط المركزية لكل مجموعة، تُحسب كمتوسط لجميع النقاط داخل المجموعة.

تعيين المجموعات: تُعين كل نقطة بيانات إلى أقرب مركز بناءً على المسافة.

خطوة التحديث: إعادة حساب المراكز بناءً على التعيينات الجديدة للمجموعات.

كيفية عمل تجميع K-Means

التهيئة: اختيار عشوائي لـ k

k نقاط من مجموعة البيانات كمراكز أولية.

التعيين: تعيين كل نقطة بيانات إلى أقرب مركز بناءً على المسافة.

التحديث: إعادة حساب المراكز عن طريق حساب متوسط النقاط ضمن كل مجموعة.

التكرار: تكرار خطوات التعيين والتحديث حتى الوصول إلى التقارب (لا تتغير المراكز بشكل ملحوظ أو يتم الوصول إلى عدد محدد من التكرارات).

النتيجة النهائية: إخراج المراكز النهائية وتعيين كل نقطة بيانات إلى مجموعة.

خصائص تجميع K-Means

التشابه الداخلي: يجب أن تكون النقاط داخل المجموعة مشابهة لبعضها البعض.

الاختلاف الخارجي: يجب أن تكون النقاط في مجموعات مختلفة متميزة.

تطبيقات تجميع K-Means

1. تقسيم العملاء

يساعد تجميع K-means الشركات على تقسيم العملاء إلى مجموعات مختلفة بناءً على ميزات مثل الدخل وسلوك الإنفاق. يتيح هذا التقسيم للشركات تخصيص استراتيجيات التسويق بشكل فعال.

2. تجميع الوثائق

في استرجاع المعلومات، يُستخدم تجميع K-means لتجميع الوثائق المماثلة معًا. يساعد هذا في تنظيم النصوص الكبيرة وتحسين نتائج البحث.

3. تقسيم الصور

يُستخدم التجميع في معالجة الصور لتقسيم الصور إلى مناطق ذات خصائص بكسل مشابهة. تكون هذه التقنية مفيدة في مجالات مثل التصوير الطبي والقيادة الذاتية.

4. محركات التوصية

من خلال تجميع المستخدمين أو العناصر بناءً على التفضيلات أو السلوك السابق، يمكن لتجميع K-means تحسين أنظمة التوصية، مما يجعلها أكثر تخصيصًا وفعالية.

معايير تقييم التجميع

1. القصور الذاتي (Inertia ) يقيس القصور الذاتي مجموع المسافات المربعة بين كل نقطة بيانات والمركز المعين لها. تشير القيم المنخفضة للقصور الذاتي إلى تجميع أفضل، حيث تكون النقاط أقرب إلى مراكزها.

2. مؤشر دون (Dunn Index)

يقيّم مؤشر دون جودة المجموعات من خلال مقارنة المسافات داخل المجموعة مع المسافات بين المجموعات. يشير مؤشر دون الأعلى إلى مجموعات مفصولة بشكل جيد وضيقة.

3. درجة السيلويت (Silhouette Score)

تقيس درجة السيلويت مدى تشابه كل نقطة مع مجموعتها مقارنةً بالمجموعات الأخرى. تتراوح الدرجات من -1 (تجميع ضعيف) إلى 1 (تجميع ممتاز)، مع 0 يشير إلى تداخل المجموعات.

من خلال التجربة العملية، يمكن أن يؤثر اختيار k

 بشكل كبير على نتيجة تجميع k-means
$$   الامثل  k تُستخدم تقنيات مثل طريقة الكوع (Elbow Method) وتحليل السيلويت (Silhouette Analysis) لتحديد 

import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

$توليد أو تحميل البيانات$

X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)

$\mathrm{<strong>تطبيق\; K-Means</strong>}$

kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)

$\mathrm{<span\; dir="LTR"><o:p><br></o:p></span><span\; dir="LTR"><strong>تصور\; المجموعات</strong></span>}$

plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75)
plt.show()

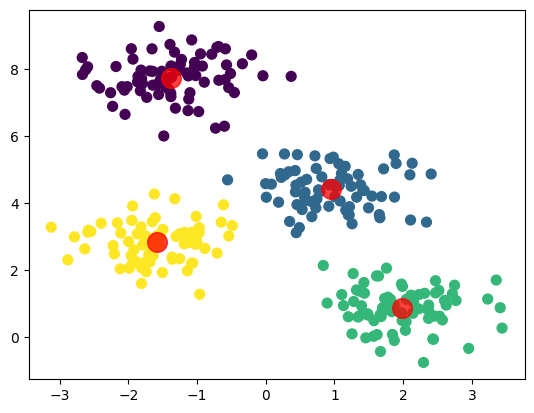
تقييم المجموعات :$\mathrm{<span\; dir="LTR"></span>}$

from sklearn.metrics import silhouette_score
silhouette_avg = silhouette_score(X, y_kmeans)
print(f'Silhouette Score: {silhouette_avg}')

Silhouette Score: 0.6819938690643478